The Alchemy of Time: A Case Study on the Compound Interest Calculator

Executive Summary

This case study explores the development, utility, and psychological impact of the compound interest calculator—a tool often cited as the most critical instrument in personal finance. By examining the mathematical foundations of exponential growth, the evolution of digital financial tools, and the behavioral shift triggered by visualizing long-term wealth, this article illustrates how a simple calculation engine serves as a catalyst for financial literacy and retirement planning.

1. Introduction: The Eighth Wonder of the World

Albert Einstein is famously quoted as calling compound interest “the eighth wonder of the world,” adding that “he who understands it, earns it; he who doesn’t, pays it.” At its core, compound interest is the interest on a loan or deposit calculated based on both the initial principal and the accumulated interest from previous periods.

While the formula is straightforward, human intuition is notoriously poor at grasping exponential growth. We tend to think linearly; we can easily imagine saving $\$500$ a month for 30 years resulting in $\$180,000$. However, we struggle to visualize that same amount, invested at a $7\%$ annual return, swelling to over $\$600,000$. The compound interest calculator bridges this cognitive gap, turning abstract mathematical theory into a tangible roadmap for wealth creation.

2. Theoretical Framework: The Mathematics of Growth

To understand the calculator, one must understand the underlying engine. The standard formula for compound interest is:

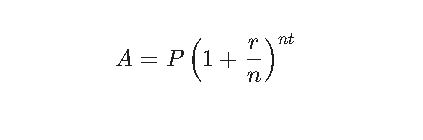
Where:

$A$ = the future value of the investment/loan, including interest.
$P$ = the principal investment amount (initial deposit).
$r$ = the annual interest rate (decimal).
$n$ = the number of times that interest is compounded per unit $t$.
$t$ = the time the money is invested or borrowed for.

2.1 The Power of Frequency ($n$)

One of the key variables modern calculators allow users to manipulate is the compounding frequency. Whether interest is compounded annually, semi-annually, quarterly, monthly, or even daily significantly affects the “yield.” Digital calculators excel at demonstrating that while the difference between monthly and daily compounding on a small scale is negligible, over decades and millions of dollars, it represents thousands in variance.

3. The Development Lifecycle of a Financial Calculator

Developing a robust compound interest calculator involves more than just implementing a formula. It requires a balance of mathematical precision, user experience (UX) design, and educational scaffolding.

3.1 Requirement Analysis

For a calculator to be effective in a modern context, it must handle:

Initial Principal: Starting balance.
Regular Contributions: Monthly or yearly additions.
Variable Time Horizons: 1 to 50+ years.
Estimated Interest Rates: Allowing for market volatility simulations.
Tax and Inflation Adjustments: Real-world purchasing power calculations.

3.2 User Interface (UI) Design

The primary challenge in financial UI is “cognitive load.” A spreadsheet is powerful but intimidating. A successful calculator uses:

Sliders: For intuitive manipulation of interest rates and time.
Dynamic Charts: Visualizing the “interest vs. principal” breakdown through stacked bar charts or area graphs.
Tables: Providing a year-by-year “schedule” for those who need granular data.

4. Behavioral Economics: The “Aha!” Moment

The true value of the compound interest calculator lies in its psychological impact. In behavioral economics, this tool is used to combat “hyperbolic discounting”—the tendency for people to choose smaller immediate rewards over larger delayed rewards.

4.1 Visualizing the “Cost of Delay”

Most advanced calculators include a feature showing the difference between starting an investment today versus waiting ten years. Seeing a $\$200,000$ “loss” in potential gains due to a decade of procrastination provides a visceral motivation that a lecture on “saving for the future” cannot.

4.2 The Tipping Point

Calculators help users identify the “crossover point”—the moment when the annual interest earned exceeds the annual contribution amount. This is a milestone in financial independence, and being able to calculate exactly when it will occur (e.g., Year 14 of a 30-year plan) transforms the abstract concept of “retirement” into a countdown to a specific event.

5. Implementation Case Study: The “Fire” Movement

The “Financial Independence, Retire Early” (FIRE) movement has been a primary driver for the proliferation of sophisticated compound interest calculators.

5.1 Case Example: The 25-Year-Old Investor

Consider a 25-year-old with a $\$10,000$ initial investment, contributing $\$1,000$ per month.

Scenario A (7% Return): At age 65, the balance is $\$2,634,000$.
Scenario B (Wait until 35): If they wait until age 35 to start, despite contributing the same monthly amount for 30 years, they end up with $\$1,227,000$.

The calculator demonstrates that a 10-year delay costs more than $\$1.4$ million, despite the total principal contributions only differing by $\$120,000$. This stark realization is often the catalyst for aggressive early-career saving.

6. Challenges and Limitations

While powerful, compound interest calculators are deterministic tools in a stochastic (random) world.

Fixed Rates of Return: Real markets do not return exactly $7\%$ every year. Sequence of returns risk—where market drops occur early in the compounding cycle—can drastically alter the outcome.
Inflation Neglect: A calculator showing $\$5$ million in 40 years is impressive, but without an inflation adjustment (e.g., $2-3\%$ annual drag), the user might over-estimate their future purchasing power.
Taxation: Most basic calculators ignore the impact of capital gains or income tax, which can erode the compounding effect significantly if the money is not in a tax-advantaged account like a 401(k) or IRA.

7. Future Trends: AI and Stochastic Modeling

The next generation of compound interest calculators is moving toward Monte Carlo Simulations. Instead of a single line of growth based on a fixed percentage, these tools run 10,000+ simulations of historical market data to provide a “probability of success.”

Instead of saying “You will have $\$2$ million,” the AI-enhanced calculator says, “Based on market history, you have an $85\%$ chance of having between $\$1.5M$ and $\$2.5M$, and a $5\%$ chance of falling below $\$800k$.” This provides a more realistic and responsible framework for financial planning.

8. Conclusion

The compound interest calculator is far more than a utility; it is an educational gateway. By translating the complex math of exponential growth into visual stories of time and discipline, it empowers individuals to take control of their financial destinies. In an era of declining pensions and increasing personal responsibility for retirement, the ability to “calculate the future” remains the most potent weapon in a saver’s arsenal.

Through the clever application of mathematics, design, and behavioral psychology, these digital tools prove that while time is fleeting, its value—when compounded—is nearly infinite.